数星星

题目

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。如果一个星星的左下方（包含正左和正下）有 k颗星星，就说这颗星星是 k级的。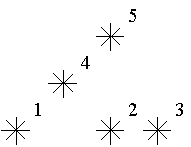
例如，上图中星星 5是 3 级的（1,2,4 在它左下），星星 2,4 是 1级的。
例图中有 1个 0 级，2 个 1 级，1 个 2 级，1 个 3级的星星。
给定星星的位置，输出各级星星的数目。
换句话说，给定 N个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。
输入格式
第一行一个整数 N，表示星星的数目；接下来 N行给出每颗星星的坐标，坐标用两个整数 x,y表示；
不会有星星重叠。星星按 y坐标增序给出，y 坐标相同的按 x坐标增序给出。
输出格式
N行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1级的星星的数目。
数据范围
1≤N≤15000,
0≤x,y≤32000
输入样例：
5
1 1
5 1
7 1
3 3
5 5
输出样例：
1
2
1
1
0

分析

首先，题中星星的坐标是先进行纵坐标，然后进行横坐标，，也就是说对于每一个星星，他的星星都是已经给出的星星中纵坐标最大的，也就是说 y 坐标是最大的，没有星星会在他的上面，所以，只需要考虑有多少个星星的横坐标是在这个星星的左侧，也就只需要考虑 x 坐标，因为树状数组从 1 开始，所以要把每一个 x 坐标加上 1

代码

#include<iostream>
#include<algorithm>
using namespace std;
int n;
int bb[32100];
int level[123456];

int lowbit(int x)
{
    return x&-x;
}

void add(int x,int c)
{
    for(int i=x;i<32100;i+=lowbit(i)) bb[i]+=c;
}

int ques(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i)) res+=bb[i];
    return res;
}

int main()
{
    int x,y;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>x>>y;
        x++;
        level[ques(x)]++;
        add(x,1);  //要先算过level之后再把这个点加上
    }
    for(int i=0;i<n;i++) cout<<level[i]<<endl;
    return 0;
}